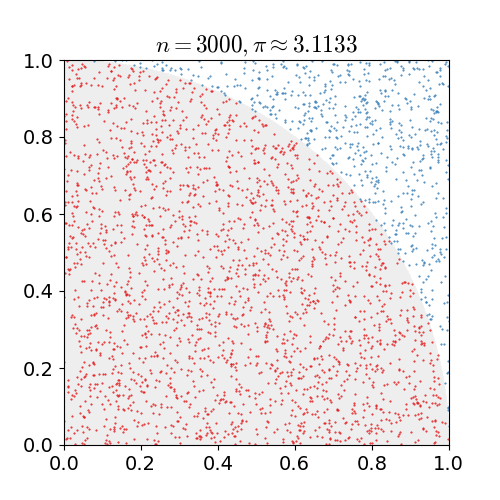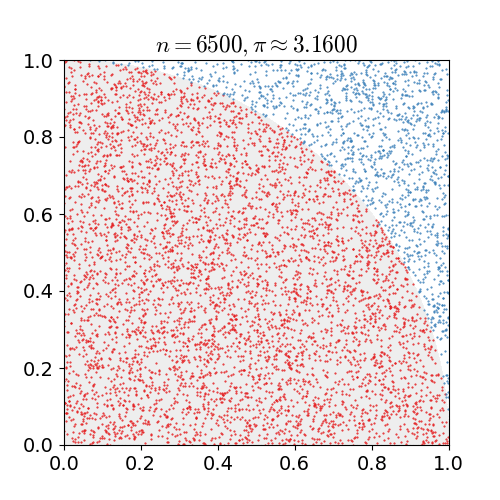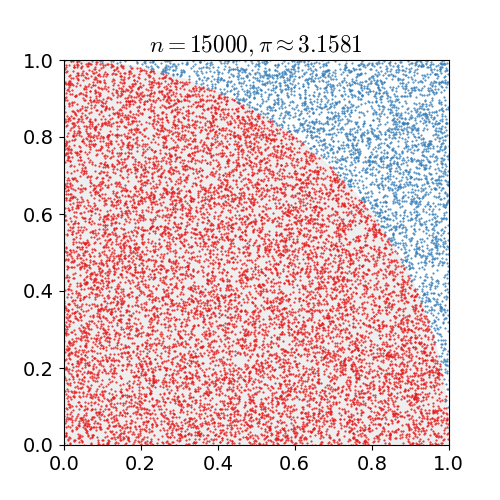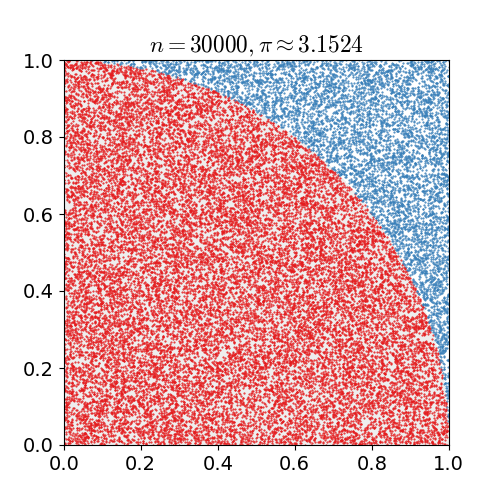
Monte Carlo method applied to approximating the value of \(\pi\). Apated from Wikipedia.

Monte Carlo in Monaco. Apated from Wikipedia.

From the book:

play with chances, either large (in terms of convergence probability) or small (in terms of winning a big prize at the Casino) chances.

From Wikipedia:

use randomness to solve problems that might be deterministic in principle.

My additional opinion:

learn through generalization.

Difference of “Monte Carlo” in statistics and computer science:

• Monte Carlo methods: target at correct (consistent) output asymptotically.
• Monte Carlo algorithms: target at incorrect output with small (non-zero) probability.

From my STAT3005 Q&A:

1. Generate data from some probabilistic models.
   • classical Monte Carlo (MC): independent random numbers.
   • Markov-Chain Monte Carlo (MCMC): a Markov chain, i.e., dependent random numbers.
2. Perform a deterministic computation on the data.
   • usually problem specific so we know what to compute in advance.
3. Aggregate the results.

For approximation of \(\pi\):

1. Generate \(U_1, U_2 \sim \mathrm{Unif}(0,1)\).
2. If \(\sqrt{U_1^2+U_2^2} \le 1\), then set \(V_i = 1\). Otherwise, set \(V_i = 0\).
   • check whether the point falls inside 1/4 of a unit circle.
3. Repeat step 1 to 2 for \(n\) times. The approximated value of \(\pi\) is \(4n^{-1} \sum_{i=1}^n V_i\).

Suppose we wish to evaluate \(\int f(x) \ \mathrm{d}x\), where \(f(x) = g(x) p(x)\). Then \[ \int_{-\infty}^\infty f(x) \ \mathrm{d}x = \int_{-\infty}^\infty g(x) p(x) \ \mathrm{d}x = \mathbb{E}\{ g(X) \}, \] where \(X \sim p\), i.e., \(X\) is a random variable whose pdf is \(p\). Under suitable conditions, the SLLN gives us \[ \bar{g}_n := \frac{1}{n} \sum_{i=1}^n g(X_i) \stackrel{\mathrm{a.s.}}{\to} \int_{-\infty}^\infty f(x) \ \mathrm{d}x, \] where \(X_1, \ldots, X_n \stackrel{\mathrm{iid}}{\sim} p\). Some notable difficulties:

1. How to simulate random replicates of \(X \sim p\)?
   • inverse transform, rejection sampling, Metropolis–Hastings, Gibbs, …
2. When to stop the simulation (at \(n = n^*\))?
3. How to improve the statistical properties of \(\bar{g}_n\)?
   • antithetic variable, stratified sampling, control variate, importance sampling, …

The book chose to introduce the Gibbs sampler first

• because it is “simpler and more intuitive for a beginner”.

I do not agree

• Gibbs is more like a divide-and-conquer strategy.
• It does not answer the fundamental question, i.e., how to simulate \(X \sim p\)?

Why MCMC instead of classical MC?

• Classical MC only applies to a restrictive range of distributions.
• Inverse transform requires:
  • finding cdf (difficult in Bayesian as only unnormalized posterior is known).
  • finding inverse of cdf (difficult in any settings).
• Rejection sampling requires:
  • optimizing the upper bound of importance ratio (not always analytical).
  • choosing a good proposal (slow for a bad proposal).

• Input: target pdf \(p(\cdot)\).
• Flow:
  1. Find the cdf \(P(\cdot)\).
  2. Find the inverse \(P^{-1}(\cdot)\).
  3. Generate \(U_i \sim \mathrm{Unif}(0,1)\).
  4. Set \(X_i = P^{-1}(U_i)\).
  5. Repeat step 3 to 4 for \(i=1,\ldots,n\).
• Output: independent data \(\{X_i\}_{i=1}^n\).

• Input:
  1. \(p(\cdot)\): target pdf.
  2. \(q(\cdot)\): proposed pdf.
• Flow:
  1. Find \(b = \max_x \{p(x)/q(x)\}\).
  2. Generate \(Y_i \sim q(\cdot)\).
  3. Generate \(U_i \sim \mathrm{Unif}(0,1)\).
  4. If \(U_i \le p(Y_i)/\{b \cdot q(Y_i) \}\), set \(X_i = Y_i\). Otherwise, restart from 2.
  5. Repeat step 2 to 4 for \(i=1,\ldots,n\).
• Output: independent data \(\{X_i\}_{i=1}^n\).

• Input:
  1. \(p_{\mathrm{u}}(\cdot)\): unnormalized target pdf.
  2. \(q(\cdot \mid \cdot)\): proposed pdf.
  3. \(p_{\mathrm{init}}(\cdot)\): initialization pdf.
• Flow:
  1. Generate \(X_0 \sim p_{\mathrm{init}}(\cdot)\).
  2. Generate \(Y_i \sim q(\cdot \mid X_{i-1})\).
  3. Generate \(U_i \sim \mathrm{Unif}(0,1)\).
  4. Compute the acceptance probability: \[ a_i = \min \left\{ \frac{p_{\mathrm{u}}(Y_i) q(X_{i-1} \mid Y_i)}{p_{\mathrm{u}}(X_{i-1}) q(Y_i \mid X_{i-1})}, 1 \right\}. \]
  5. Set \(X_i = Y_i \mathbb{1}(U_i \le a_i) +X_{i-1} \mathbb{1}(U_i > a_i)\).
  6. Repeat step 2 to 5 for \(i=1,\ldots,n\).
• Output: Markov chain \(\{X_i\}_{i=1}^n\).

What if \(p(\cdot)\) is a \(d\)-dimensional pdf?

• \(\boldsymbol{X}\) is normal: Cholesky decomposition/spectral decomposition.
• \(\boldsymbol{X}\) is not normal: no general methods.
  • rejection rate can be high for rejection sampling and MH.
• Gibbs provides a general framework for multivariate sampling.
  • essentially, Gibbs breaks down the problem into at most \(d\) univariate problems.
  • univariate simulation is well-studied.
• Let’s review some facts before we proceed.
  • the joint is fully recoverable from the conditionals.
  • except special cases such as independence, the joint is not recoverable from the marginals.
  • Gauss–Seidel algorithm shares similar ideas as the Gibbs sampler.

• Denote the joint, marginal and conditional pdf’s of X and Y by \(p(x,y)\), \(p_X(x)\), \(p_Y(y)\), \(p_{X \mid Y}(x \mid y)\) and \(p_{Y \mid X}(y \mid x)\).
• Note that \[ p(x,y) = p_{X \mid Y}(x \mid y) p_Y(y) = p_{Y \mid X}(y \mid x) p_X(x) \implies \frac{p_Y(y)}{p_X(x)} = \frac{p_{Y \mid X}(y \mid x)}{p_{X \mid Y}(x \mid y)}. \]
• Therefore, we have \[ \begin{aligned} p(x,y) &= p_{Y \mid X}(y \mid x) p_X(x) \\ &= \frac{p_{Y \mid X}(y \mid x) p_X(x)}{\int_{-\infty}^\infty p_Y(y) \ \mathrm{d}y} \\ &= p_{Y \mid X}(y \mid x) \left\{ \int_{-\infty}^\infty \frac{p_Y(y)}{p_X(x)} \ \mathrm{d}y \right\}^{-1} \\ &= p_{Y \mid X}(y \mid x) \left\{ \int_{-\infty}^\infty \frac{p_{Y \mid X}(y \mid x)}{p_{X \mid Y}(x \mid y)} \ \mathrm{d}y \right\}^{-1}. \end{aligned} \]

• Having something done component-wisely and iteratively is not new.
• Suppose we want to solve a large system of equations expressed as \[ L(x^{(1)}, \ldots, x^{(d)}) = 0. \]
• Let \(L_i\) be the \(i\)-th component of \(L\). The Gauss–Seidel algorithm is
  1. Initialize \(\boldsymbol{x}_0 = (x_0^{(1)}, \ldots, x_0^{(d)})^\intercal\).
  2. Solve \(x_i^{(1)}\) from \(L_1(x^{(1)}, x_{i-1}^{(2)}, \ldots, x_{i-1}^{(d)}) = 0\).
  3. Similarly, solve \(x_i^{(2)}\) from \(L_2(x_i^{(1)}, x^{(2)}, \ldots, x_{i-1}^{(d)}) = 0\).
  4. Repeat step 3 to solve \(x_i^{(k)}\) for \(k=3, \ldots, d\).
  5. Repeat step 2 to 4 for \(i=1, \ldots, n\).
• Under mild conditions, \(\boldsymbol{x}_n\) converges globally regardless of \(\boldsymbol{x}_0\).

• Adapted from Keith’s STAT4010 notes.
• Input:
  1. \(p^{(k \mid -k)}(\cdot \mid x^{(-k)})\): conditional pdf for \(k=1,\ldots,d\).
  2. \(p_{\mathrm{init}}(\cdot)\): initialization pdf.
• Flow:
  1. Generate \(\boldsymbol{Y} \sim p_{\mathrm{init}}(\cdot)\).
  2. Set \(\boldsymbol{X}_i = \boldsymbol{Y}\).
  3. Generate \(Y^{(k)} \sim p^{(k \mid -k)}(\cdot \mid X_i^{(-k)})\).
  4. Set \(X_i^{(k)} = Y^{(k)}\).
  5. Repeat step 3 to 4 for \(k=1,\ldots,d\).
  6. Repeat step 2 to 5 for \(i=1,\ldots,n\).
• Output: Markov chain \(\{\boldsymbol{X}_i\}_{i=1}^n\).

(Theorem 15.1) Suppose that the Markov chain has transition kernel \(K\) and stationary distribution \(\pi\) so that \(K\) is \(\pi\)-irreducible and aperiodic. Then, for all \(x \in D=\{x: \pi(x) > 0\}\), the following hold:

1. \(\int_{-\infty}^\infty |K_t(x, v) -\pi(v)| dv \to 0\) as \(t \to \infty\).
   • \(K_t(x,\cdot)\) is the transition kernel for \(X_t\) given \(X_0 = x\).
2. For any real-valued, \(\pi\)-integrable function \(g\), \[ \frac{1}{n} \sum_{t=1}^n g(X_t) \stackrel{\mathrm{a.s.}}{\to} \int_{-\infty}^\infty g(x) \pi(x) \ \mathrm{d}x. \]

(Theorem 15.2) The conditions of Theorem 15.1 hold for the Gibbs sampler provided that \(F\) is lower semicontinuous at zero, \(D\) is connnected, and both \(f_X(\cdot)\) and \(f_Y(\cdot)\) are locally bounded.

• \(F\) is the cdf of \(f(x,y)\) as a bivariate case is considered in the book.

Suppose we simulate \(\boldsymbol{X} = (X^{(1)}, X^{(2)}, X^{(3)})^\intercal\) with Gibbs. Some possible strategies are:

• Direct: sample from \(p^{(k \mid -k)}\), \(k=1,2,3\).
• Grouping: sample \(X^{(1)}\) from \(p^{(1 \mid 2,3)}\) and \(X^{(2)}, X^{(3)}\) from \(p^{(2,3 \mid 1)}\).
  • possible if we can draw \(X^{(2)}\) from \(p^{(2 \mid 1)}\) and \(X^{(3)}\) from \(p^{(3 \mid 1,2)}\).
  • as known as blocked Gibbs sampler.
• Collapsing: omit \(X^{(3)}\), and sample \(X^{(1)}\) from \(p^{(1 \mid 2)}\) and \(X^{(2)}\) from \(p^{(2 \mid 1)}\)
  • sampling from \(p^{(1 \mid 2)}\) is generally tractable when \(X^{(3)}\) is a conjugate prior of \(X^{(1)}\); see Wikipedia.
  • sensible if the problem of interest only involves the joint of \(X^{(1)}\) and \(X^{(2)}\).

Which strategy is the best?

• Traditional investigation: (advanced) theory of Markov chains.
  • e.g., Geman and Geman (1984), Nummelin (1984) and Tierney (1991).
• “Elementary” approach: simple functional analysis and inequalities.
  • e.g., Liu (1994) and Liu et al. (1994, 1995).

• Hilbert space considered: \(L_0^2(f) = \{g(X): \mathbb{E}\{g(X)\} = 0\ \mathrm{and}\ \mathbb{E}\{|g(X)|^2\} < \infty \}\).
• Inner product: \(\langle g(X),h(X) \rangle = \mathbb{E}\{ g(X) \overline{h(X)} \}\).
  • complex conjugate: \(\overline{c}\); modulus: \(|c|\).
• Variance: \(\left\lVert g(X)\right\rVert^2 = \langle g(X),g(X) \rangle = \mathbb{E}\{ |g(X)|^2 \}\).
• Pearson \(\chi^2\)-discrepancy between \(p\) and \(q\): \[ d_p^2(q,p) = \int_{-\infty}^\infty \left\{ \frac{q^2(x)}{p(x)} \right\} \ \mathrm{d}x -1 = \mathrm{Var}\left\{ \frac{q(X)}{p(X)} \right\}. \]
  • \(d_p\) is nonnegative but not a distance.
  • \(d_p\) can be shown as a stronger measure of discrepancy than \(\mathcal{L}^1\)-distance.
  • \(d_p\) is also a stronger meausre than certain kind of Kullback–Leibler information distance.

• Forward operator \(\mathbf{F}\) (with \(K\) as the transition kernel): \[ \mathbf{F} g(X) = \mathbb{E}\{ g(X_1) \mid X_0 = X \} = \int_{-\infty}^\infty g(y) K(X,y) \ \mathrm{d}y. \]
• Norm of \(\mathbf{F}\): \[ \left\lVert\mathbf{F}\right\rVert = \sup_{g \in L_0^2(f), \left\lVert g\right\rVert = 1} \left\lVert\mathbf{F} g\right\rVert \]
• Results of Liu et al. (1994): \[ \left\lVert\mathbf{F}_{\mathrm{collapse}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{group}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{direct}}\right\rVert \]
  • smaller \(\left\lVert\mathbf{F}\right\rVert\), faster convergence.
  • expected as collapsing and grouping require more manual work.

• Let \(p_t\) denote the pdf of \(X_t\). By the Markovian property, \[ \begin{aligned} \mathbb{E}_{p_t}\{ g(X) \} &= \int_{-\infty}^\infty \int_{-\infty}^\infty g(y) K(x,y) p_{t-1}(x) \ \mathrm{d}x \ \mathrm{d}y, \\ \mathbb{E}_p\{ g(X) \} &= \int_{-\infty}^\infty \int_{-\infty}^\infty g(y) K(x,y) p(x) \ \mathrm{d}x \ \mathrm{d}y. \end{aligned} \]
• It follows that \[ \begin{aligned} \mathbb{E}_{p_t}\{ g(X) \} -\mathbb{E}_p\{ g(X) \} &= \int_{-\infty}^\infty \int_{-\infty}^\infty g(y) K(x,y) \left\{ \frac{p_{t-1}(x)}{p(x)} -1\right\} p(x) \ \mathrm{d}x \ \mathrm{d}y \\ &= \int_{-\infty}^\infty \mathbf{F} g(x) \left\{ \frac{p_{t-1}(x)}{p(x)} -1\right\} p(x) \ \mathrm{d}x. \end{aligned} \]
• By the Cauchy–Schwarz inequality, we have (15.28) in the book: \[ \left| \mathbb{E}_{p_t}\{ g(X) \} -\mathbb{E}_p\{ g(X) \} \right| \le \left\lVert\mathbf{F} g(X)\right\rVert d_p(p_{t-1},p) \le \left\lVert\mathbf{F}\right\rVert \cdot \left\lVert g(X)\right\rVert d_p(p_{t-1},p). \]

• Note that \[ \int_{-\infty}^\infty \left\{ \frac{p_{t-1}(x)}{p(x)} -1\right\}^2 p(x) \ \mathrm{d}x = d_p^2(p_{t-1},p). \]
• Consider \(g(X) = p_t(X)/p(X)-1\). We have \(\mathbb{E}\{g(X)\} = 0\) and \[ \mathbb{E}\{g(X)^2\} = \int_{-\infty}^\infty \left\{ \frac{p_t(x)}{p(x)} -1\right\}^2 p(x) \ \mathrm{d}x = d_p^2(p_t,p). \]
• If \(d_p^2(p_t,p)\) is finite, we can obtain (from (15.28) in the book; see last page): \[ d_p(p_t,p) \le \left\lVert\mathbf{F}\right\rVert d_p(p_{t-1},p), \]
  • which holds for all \(t\) as long as \(d_p^2(p_t,p) < \infty\).

• Therefore, if \(d_p^2(p_{t_0},p) < \infty\), we have for any \(t \ge t_0\) that \[ \begin{aligned} d_p(p_t,p) &\le \left\lVert\mathbf{F}\right\rVert d_p(p_{t-1},p) \\ &\le \left\lVert\mathbf{F}\right\rVert^2 d_p(p_{t-2},p) \\ &\ \ \vdots \\ &\le \left\lVert\mathbf{F}\right\rVert^{t-t_0} d_p(p_{t_0},p) \\ &= c_0 \left\lVert\mathbf{F}\right\rVert^t, \end{aligned} \]
  • where \(c_0 = d_p(p_{t_0},p)/\left\lVert\mathbf{F}\right\rVert^{t_0}\).
• This suggested that the convergence rate of the Markov chain is closely related to \(\left\lVert F\right\rVert\).
  • combine with \(\left\lVert\mathbf{F}_{\mathrm{collapse}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{group}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{direct}}\right\rVert\).
  • collapsing is better than grouping, which, in turn, is better than the direct Gibbs sampler.
• However, we cannot simply conclude based on the convergence rate.
  • other factors include computational efficiency and (manual) simplicity.

How to prove the inequality \(\left\lVert\mathbf{F}_{\mathrm{collapse}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{group}}\right\rVert \le \left\lVert\mathbf{F}_{\mathrm{direct}}\right\rVert\)?

• Relate \(\left\lVert\mathbf{F}\right\rVert\) to the maximum correlation, which is defined as \[ \rho(\boldsymbol{X},\boldsymbol{Y}) = \sup_{g,h: \mathrm{Var}\{g(\boldsymbol{X})\} <\infty, \mathrm{Var}\{h(\boldsymbol{Y})\} <\infty} \mathrm{Corr}\{ g(\boldsymbol{X}), h(\boldsymbol{Y}) \}. \]
• A useful alternative expression is given by \[ \{ \rho(\boldsymbol{X},\boldsymbol{Y}) \}^2 = \sup_{g: \mathrm{Var}\{g(\boldsymbol{X})\}=1} \mathrm{Var}[\mathbb{E}\{ g(\boldsymbol{X}) \mid Y\}]. \]
• We have the relation: \[ \left\lVert\mathbf{F}\right\rVert = \rho(\boldsymbol{X}_0, \boldsymbol{X}_1). \]
• See the book and Liu et al. (1994) for the complete proof.

Briefly discussed in my STAT4010 tutorial:

1. Expectation–maximization (EM) algorithm
   To obtain MLE, we need to optimize the likelihood function, which may not have closed form in some models. In that case, we may replace the expectation step in the EM algorithm with a MCMC procedure; see the description here.

2. Stochastic approximation (SA) algorithm
   Instead of using MCMC and Riemann sum to approximate an expectation, we can use MCMC to generate the required random effect in the SA algorithm; see the description here. (Perhaps the most well-known SA algorithm is the stochastic gradient descent)

3. Machine learning
   MC or MCMC methods can be used to enhance or even construct machine learning algorithms. For example, the algorithm behind AlphaGo includes Monte Carlo tree search.